Autómata finito determinista y no determinista
Autómatas Finitos Determinista (AFD)
Un AFD tiene un conjunto finito de estados y un conjunto finito de símbolos de entrada. El término “determinista” hace referencia al hecho de que para cada entrada sólo existe uno y sólo un estado al que el autómata puede hacer la transición a partir de su estado actual. Un estado se diseña para que sea el estado inicial, y cero o más estados para que sean estados de aceptación. Una función de transición determina cómo cambia el estado cada vez que se procesa un símbolo de entrada.
Un autómata finito determinista consta de:
- Un conjunto finito de estados, a menudo designado como 𝑄.
- Un conjunto finito de simbolos de entrada, a menudo designado como 𝛴
- Una función de transición que toma como argumentos un estado y un símbolo de entrada y devuelve un estado. la funcion de transicion se designa habitualmente como 𝛿. En nuestra representación gráfica informal del autómata, 𝛿 se ha representa mediante arcos entre los estados y las etiquetas sobre los arcos. Si q es un estado y a es un símbolo de entrada, entonces 𝛿(q,a) es el estado p tal que existe un arco etiquetado a que va desde q hasta p.
- Un estado inicial, uno de los estados de Q.
- Un conjunto de estados finales o de aceptación F. El conjunto F es un subconjunto de Q.
Procesamiento de las cadenas de un AFD
Lo primero que tenemos que entender sobre un AFD es cómo decide si “aceptar” o no una secuencia de símbolos de entrada. El “lenguaje” del AFD es el conjunto de todas las cadenas que acepta. Supongamos que a1,a2,...,an es una secuencia de símbolos de entrada. Comenzaremos con el AFD en el estado inicial, q0. Consultamos la función de transición δ, por ejemplo δ(q0,a1)=q1 para hallar el estado al que pasará el AFD A después de procesar el primer símbolo de entrada a1. A continuación procesamos el siguiente símbolo de entrada, a2, evaluando δ(q1,a2);supongamos que este estado es q1. Continuamos aplicando el mismo procedimiento para hallar los estados q3,q4,...,qn tal que δ(qi-1,a1)=qi para todo i. Si qn pertenece a F, entonces la entrada a1,a2,..., an se acepta y, si no lo es se “rechaza”.
Notaciones
Especificar un AFD utilizando una quíntupla con una descripción detallada de la función de transición δ resulta bastante tedioso y complicado de leer. Hay disponibles dos notaciones más cómodas para describir los autómatas:
Diagrama de transiciones:
Los diagramas de transición son adecuados para representar autómatas mediante un grafo en el que los nodos son los estados y los arcos se etiquetan con los símbolos de entrada, indicando las transiciones de dicho autómata. El estado inicial se designa mediante una flecha y los estados de aceptación mediante círculos dobles.
Tablas de transiciones
Una tabla de transiciones es una representación tabular convencional de una función, como por ejemplo δ , que toma dos argumentos y devuelve un valor. Las filas de la tabla corresponden a los estados y las columnas a las entradas. La entrada para la fila correspondiente al estado q y la columna correspondiente a la entrada a es el estado δ (q,a).
Ejemplo:
La tabla de transiciones correspondiente a la función δ del Ejemplo se muestra en la Figura 2.5. También pueden verse otras dos características de una tabla de transiciones. El estado inicial se marca mediante una flecha y los estados de aceptación mediante un asterisco. Dado que es posible deducir los conjuntos de estados y los símbolos de entrada fijándose en los encabezamientos de las filas y las columnas, podemos obtener a partir de la tabla de transiciones toda la información necesaria para especificar el autómata finito de forma unívoca.
Autómatas Finitos No Determinista
Un Autómata finito determinista queda definido por un quíntupla, al igual que en los AFD, y que su diferencia fundamental se encuentra, en cómo se definirá a la función de transición:
AFND = ( ∑ , Q, q0, F, f )
donde:
∑ | Alfabeto de símbolos de entrada. |
Q | Conjunto finito de estados |
q0 | qo |
F | F |
f | Función de transición de estados definida como f: Q x (∑ U { En donde P (Q), es el conjunto que se puede armar con todos los subconjuntos de Q |


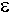
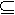
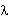 } ) → P (Q)
} ) → P (Q)
Comentarios
Publicar un comentario